Graphes
Un graphe est un ensemble de sommets et d'arêtes. C'est un outil permettant de représenter des objets (sommets) et des liens ou interactions entre ces objets (arêtes), par exemple : le réseau SNCF, les villes/routes, les réseaux et les labyrinthes. Les graphes peuvent permettre de trouver les sorties de labyrinthe. On peut, pour expliciter leur intérêts, utiliser les graphes avec l'exemple du berger:
Un berger a un loup, une chèvre et un chou. En présence du berger, la chèvre ne mange pas le chou et le loup ne mange pas la chèvre. Pour traverser une rivière, le berger ne peut transporter qu'un seul de ces compagnons avec lui.
Il y a donc 16 combinaisons possibles pour ces 4 objets. Chaque combinaison sera représentée par l'état de la rive de départ. Chaque combinaison est un sommet, chaque arête est un trajet.
Combinaisons impossibles :
-Chèvre-chou
-Loup-chèvre
-Loup-berger
-Chou-berger
-Les 3
-Berger
Combinaisons possibles:
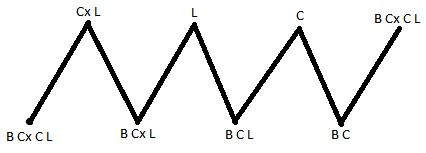
Un labyrinthe peut-être
décrit par un graphe, les croisements étant les objets placés aux
sommets et les couloirs, les liens entre ces sommets. Entrée A / Sortie Z :
1 A
2 AB
3 ABC / ABM
4 ABCD / ABCK / ABM
5 ABCDE / ABCDK / ABCK / ABM
6 ABCDEG / ABCDEF / ABCK / ABM
7 ABCDEGI / ABCDEGH / ABCK / ABM
8 ABCDEGIJ / ABCK / ABM
9 ABCKL / ABCKD / ABM
10 ABMN / ABMZ (Exploration en profondeur)
OU
Le parcours d'un graphe en largeur traite d'abord les possibilités les plus courtes.
1 A
2 AB
3 ABC / ABM
4 ABCD / ABCK / ABM (car plus court)
5 ABMN / ABMZ / ABCD / ABCK (Exploration en largeur)
En conclusion, le parcours en largeur permet de trouver le chemin le plus court tandis que le parcours en profondeur, pour ne pas tourner en rond, doit interdire de repasser par des sommets déjà utilisés.
